精选推荐 ▏学会旗舰会刊《CSIAM Transactions on Applied Mathematics》2025年精选文章(一)
《CSIAM Transactions on Applied Mathematics》(CSIAM-AM)是中国工业与应用数学学会的旗舰期刊。该期刊发表应用数学、计算数学或科学计算领域的高质量原创研究论文。CSIAM-AM由中国工业与应用数学学会前任理事长、武汉大学校长张平文院士担任主编,中国工业与应用数学学会理事长、浙江大学求是讲席教授包刚院士担任总编辑。
2025年,CSIAM-AM刊发学术论文28篇。本刊精选9篇代表作,分三期陆续呈现。本期首期聚焦三篇佳作,诚邀专家学者深入研读,共同探讨前沿新知。
01
A Variational Discretization Method for Mean Curvature Flows by the Onsager Principle
Yihe Liu, Xianmin Xu
CSIAM Trans. Appl. Math., 6 (1), pp. 63-95.
DOI: https://doi.org/10.4208/csiam-am.SO-2024-0005
文章介绍:
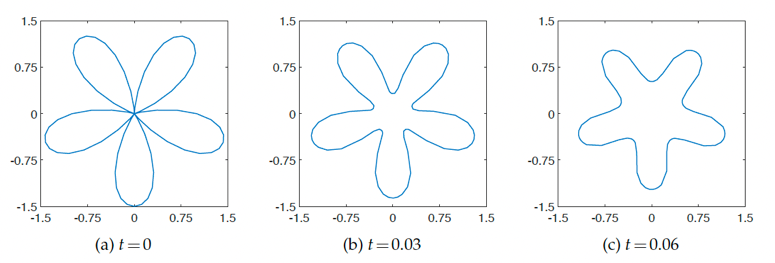
平均曲率流是一类典型的几何流问题,在数学、材料科学以及工程等领域有着广泛应用。因为其高度非线性和求解区域不断随时间演化,对平均曲率流发展稳定高效数值格式和误差估计都比较困难。本文基于Onsager变分原理发展了一种新型的变分离散方法。我们首先建立连续平均曲率流与 Onsager 变分原理的联系;随后,通过将连续曲线进行分片线性近似,我们利用该变分原理推导离散曲线结点演化的常微分方程组,证明了半离散系统保持连续问题的能量耗散结构;最后,我们在能量泛函中引入罚项,采用改进欧拉格式离散时间导数,构建了一个全离散格式。我们还将该方法推广应用于体积守恒的平均曲率流和浸润问题。数值实验表明,该方法能够保持良好网格质量并且具有最优收敛性。这项研究为复杂几何流方程的数值方法设计和分析打开了新思路。
02
Haifeng Wang, Jingwei Sun, Hong Zhang, Xu Qian
CSIAM Trans. Appl. Math., 6(1), 106-147.
DOI: https://doi.org/10.4208/csiam-am.SO-2024-0032
文章介绍:
材料冷却、晶体生长、薄膜延展……这些看似不同的过程,背后都遵循“能量递减”这一共性规律,可由梯度流模型统一刻画。然而其数值模拟长期面临高精度、保结构和高效率无法兼得的“三角矛盾”。
该学校保结构算法研究团队重构Lawson积分因子方法,提出保稳态指数算子高阶逼近理论,解决指数衰减因子造成奇异界面过度光滑难题(图1),从数学本质上克服稳态畸变和高频阻尼(图2),突破已有无条件能量耗散算法的三阶精度瓶颈,系统提出四阶线性、无条件保持原始能量耗散的指数龙格-库塔算法,让强刚性问题“算得准、算得稳、算得快”。该框架的系列推广可无条件保持Allen-Cahn类型方程的最大模上界原理[Comput. Methods Appl. Mech. Engr., 2022, 393: 114817]和双曲守恒律的强稳定性[Commun. Comput. Phys., 2024, 35(2): 498-523]。
论文作者为王海峰、孙竟巍、张弘、钱旭。研究工作得到了国家自然科学基金、国家重点研发计划、湖南省科技创新计划等项目的支持。
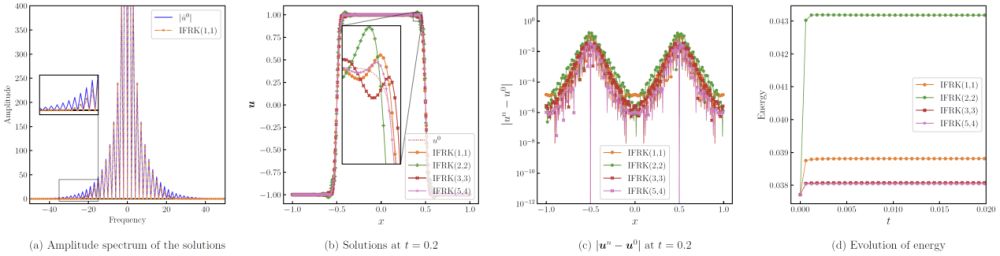
图1 经典积分因子龙格-库塔格式(IFRK)的高频阻尼(a)过度光滑奇异界面(b),界面处误差大(c)且无法保持能量耗散(d)
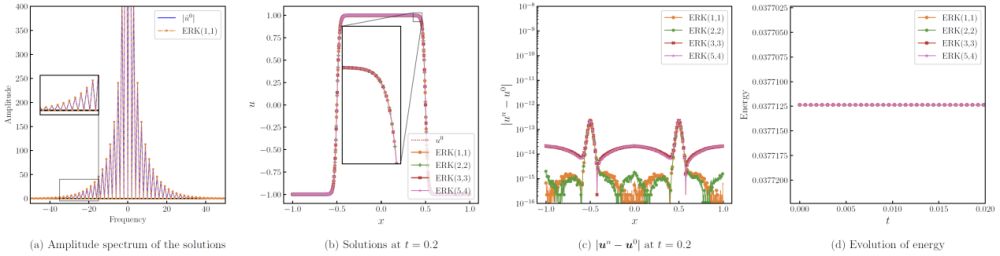
图2 保稳态指数龙格-库塔格式克服高频阻尼(a)带来的稳态畸变(b),界面误差达到机器精度(c)且严格保持能量耗散(d)
03
Computational Imaging of Small-Amplitude Biperiodic Surfaces with Negative Index Material
Yuliang Wang
CSIAM Trans. Appl. Math.,6(1), 148-175.
DOI: https://doi.org/10.4208/csiam-am.SO-2024-0008
文章介绍:
在波动成像领域,分辨率通常受制于阿贝衍射极限:测量点距离目标越远,能携带细节信息的“倏逝波”衰减越快,因此难以恢复亚波长尺度的结构。本研究提出一种结合负折射率超透镜的计算成像方法,用以重建双周期粗糙表面(如二维衍射光栅)的微小起伏形状,实现了远超波长限制的成像精度。
负折射率材料能够在界面附近放大倏逝波,理论上可实现“无限分辨率”。本工作首次将这种物理机制系统地融入计算成像框架中:通过构建完整的波动模型、引入坐标变换及渐近展开,推导出一个简单而精确的重建公式,可直接将测量场的傅里叶系数转换为表面的几何信息。
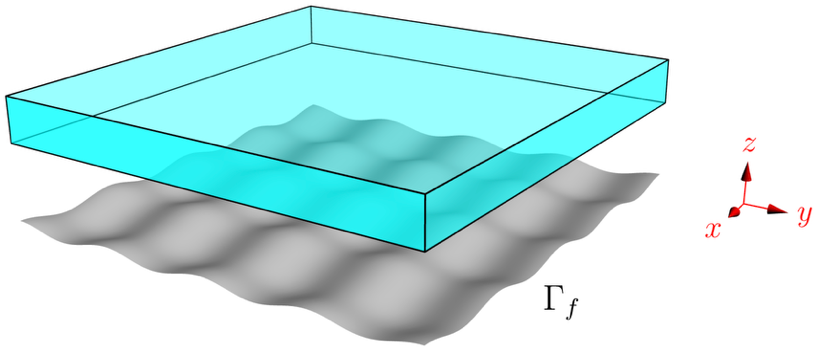
图3 超透镜辅助的双周期表面计算成像示意图。超透镜位于粗糙表面上方,通过放大倏逝波,将表面的高频细节传递至测量面,为突破衍射极限奠定基础。
数值实验表明,即便材料存在轻微损耗、测量数据含噪声,方法依然能稳定恢复表面的高频细节,在多种光滑与非光滑表面上均取得显著超过衍射极限的成像效果。
本研究为将超透镜与计算成像深度融合提供了新的数学模型与数值框架,也为未来在声学、光学及电磁波成像中的亚波长探测奠定了基础。
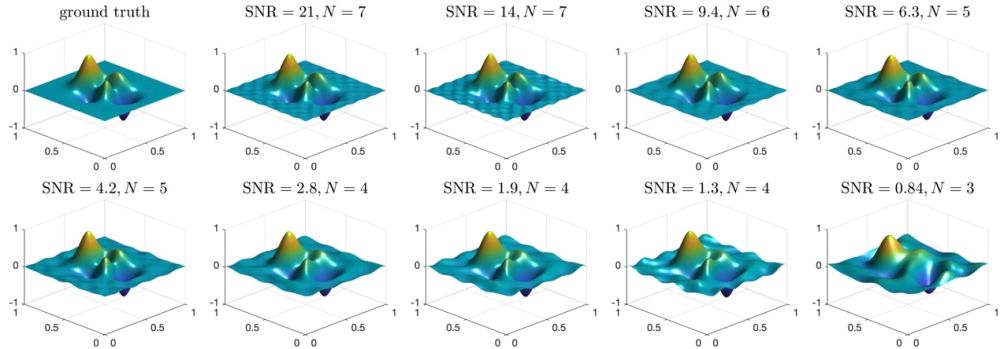
图4 超透镜辅助的表面重建结果示例。SNR:信噪比,N:算法提供的截断频率。
期刊官网:https://global-sci.org/index.php/csiam-am。
《CSIAM Transactions on Applied Mathematics》欢迎大家积极投稿,投稿网址: https://mc03.manuscriptcentral.com/csiam。
学会出版委员会供稿




