《CSIAM Transactions on Applied Mathematics》（CSIAM-AM）是中国工业与应用数学学会的旗舰期刊。该期刊发表应用数学、计算数学或科学计算领域的高质量原创研究论文。CSIAM-AM由中国工业与应用数学学会前任理事长、武汉大学校长张平文院士担任主编，中国工业与应用数学学会理事长、浙江大学求是讲席教授包刚院士担任总编辑。

2025年，CSIAM-AM刊发学术论文28篇。继上期三篇佳作，本期再推三篇精选。诚邀专家学者深入研读，共同探讨前沿新知。

01

Review of Mathematical Optimization in Federated Learning

Shusen Yang, Fangyuan Zhao, Zihao Zhou, Liang Shi, Xuebin Ren, Zongben Xu

CSIAM Trans. Appl. Math., 6(2), 207-249.

DOI: https://doi.org/10.4208/csiam-am.SO-2024-0023

文章介绍：

本研究系统综述联邦学习中的数学优化问题，如图1所示。联邦学习作为一种隐私保护分布式机器学习范式，其系统架构如图2所示，当前面临四大核心挑战：异构数据导致的局部偏差、差分隐私产生的梯度误差、去中心架构泛化性低、以及动态数据流中的模型过时与灾难性遗忘。针对上述挑战，系统性地综述了优化方案：通过正则化、方差缩减等校正数据异构偏差；优化梯度裁剪、隐私放大采样等技术平衡隐私与精度；通过拓扑感知优化提升泛化性和收敛率；引入核方法与记忆回放机制应对动态环境；并涵盖稀疏化通信与鲁棒聚合等方向。本研究填补了联邦学习优化理论空白，致力于实现效用、效率与隐私的最优权衡，为医疗、金融等高敏场景的跨域协作提供理论支撑，助力隐私合规与数据高效利用。

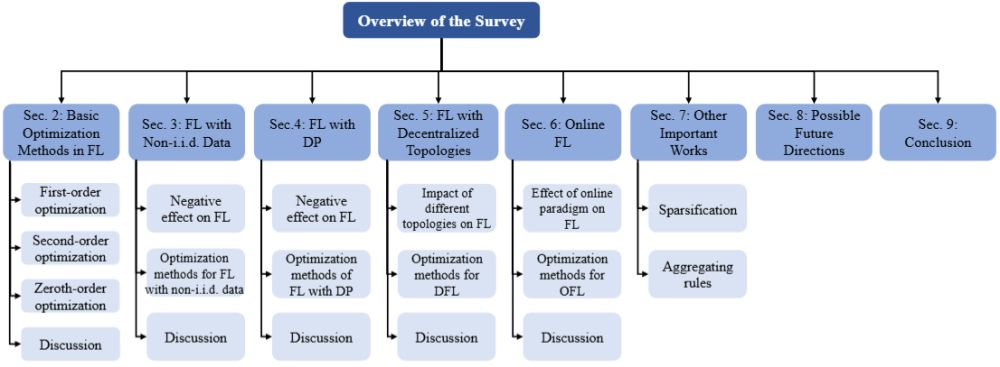
图1 综述框架概览

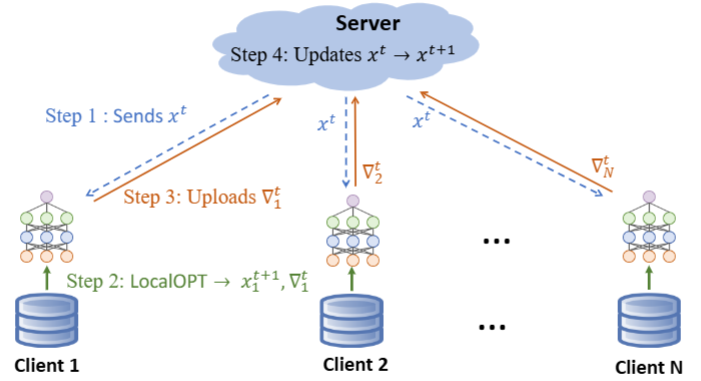
图2 联邦学习系统架构图

02

ℓ₁DecNet+: A New Architecture Framework by ℓ₁ Decomposition and Iteration Unfolding for Sparse Feature Segmentation

Yumeng Ren, Yiming Gao, Xue-Cheng Tai, Chunlin Wu

CSIAM Trans. Appl. Math., 6(2), 250-271.

DOI: https://doi.org/10.4208/csiam-am.SO-2024-0033

文章介绍：

稀疏特征目标分割是一个有别于其它图像分割任务的困难问题，其待分割目标呈现尺寸小、分布散等特点。以往的方法在争取高精度效果的同时，存在计算量大或可解释性不足等缺陷。本文的理念是对待分割目标的特征的精确刻画，将有助于后续的分割任务。本文提出一种基于变分分解模型的迭代展开神经网络ℓ₁DecNet（见图3，来自本文），通过融合ℓ₁稀疏正则化与非标准缩放型交替方向乘子法（ADMM），构建可学习的特征分解框架，将待分割目标和图像背景部分分离处理，自适应地从原始图像中解耦稀疏特征与复杂稠密特征；在此基础上构建由特征分解模块与面向稀疏特征的分割模块级联而成的ℓ₁DecNet+架构（见图3），实现了数学先验建模与深度学习方法的有机结合。不同于以往的图像分割架构，该研究将数学图像底层视觉先验嵌入分割过程的特征提取层，充分利用了待分割目标的稀疏特性和背景图像的可学习稀疏化表示。在多个公开数据集上的实验表明：ℓ₁DecNet+提供高精度分割的同时（见表1，来自本文），大幅减少可学习参数规模，具有推理效率高、可解释性强等优点。该方法是一个面向稀疏目标分割的基础性框架，可应用于视网膜血管分割、路面裂缝检测、工业缺陷检测等问题。

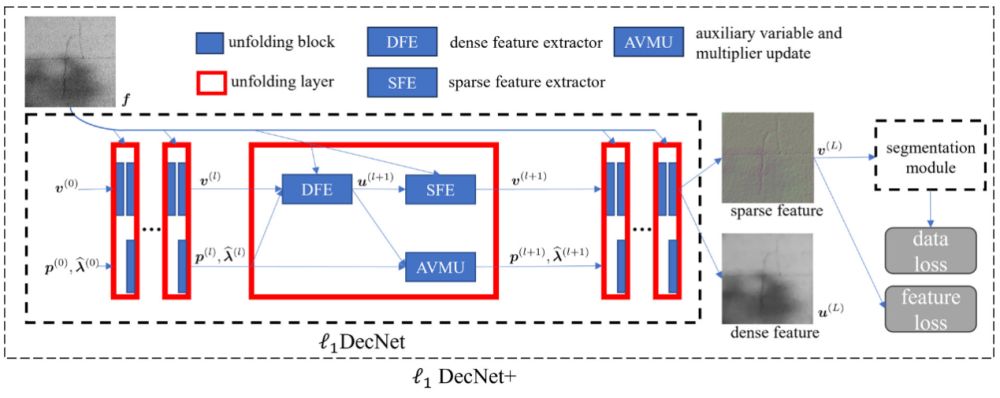
图3 ℓ₁DecNet与ℓ₁DecNet+架构

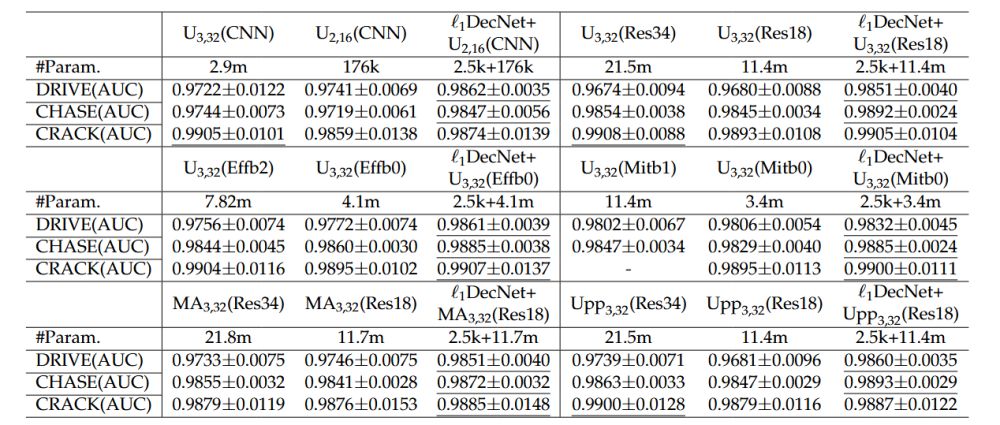
表1 ℓ₁DecNet用于构建性能优秀的轻量级稀疏特征分割模型ℓ₁DecNet+架构

03

A Constrained BA Algorithm for Rate-Distortion and Distortion-Rate Functions

Lingyi Chen, Shitong Wu, Wenhao Ye, Huihui Wu, Wenyi Zhang, Hao Wu, Bo Bai

CSIAM Trans. Appl. Math.,6(2), 350-379.

DOI: https://doi.org/10.4208/csiam-am.SO-2024-0002

文章介绍：

针对信息论中的经典重要问题——率失真函数计算，本文提出了一种最优输运理论启发的Constrained Blahut–Arimoto（CBA）算法。率失真函数刻画了失真约束下，信息表征效率的理论极限。其经典计算方法基于固定拉格朗日乘子，需要通过参数扫描逼近目标失真，在应用中常导致收敛缓慢与数值不稳定等困难。

本文注意到率失真理论与最优输运在数学形式上的对应，将信息表征视为“质量传输”，其失真约束对应于最优输运中的质量上界。基于此对应关系，本文通过推广Sinkhorn 算法设计了CBA算法，将乘子寻优转化为单变量单调方程求根问题，实现了对任意目标失真的直接高效计算。CBA算法具有可证明的线性收敛速度，计算效率较基准方法提升了一至两个数量级，并克服了在分岔点附近的数值失效问题。

本工作为率失真函数计算提供了新的数学工具与算法框架，其思路还可拓展至信息瓶颈、误匹配译码等其他信息论重要问题，形成高效且稳健的数值求解统一路径。

期刊官网：https://global-sci.org/index.php/csiam-am。

《CSIAM Transactions on Applied Mathematics》欢迎大家积极投稿，投稿网址: https://mc03.manuscriptcentral.com/csiam。

 学会出版委员会供稿